Instant Transport Maps on 2D Grids

Georges Nader ¹ , Gael Guennebaud ¹

1. Inria - Bordeaux University - LaBRI

ACM Transactions on Graphics (Siggraph Asia 2018)

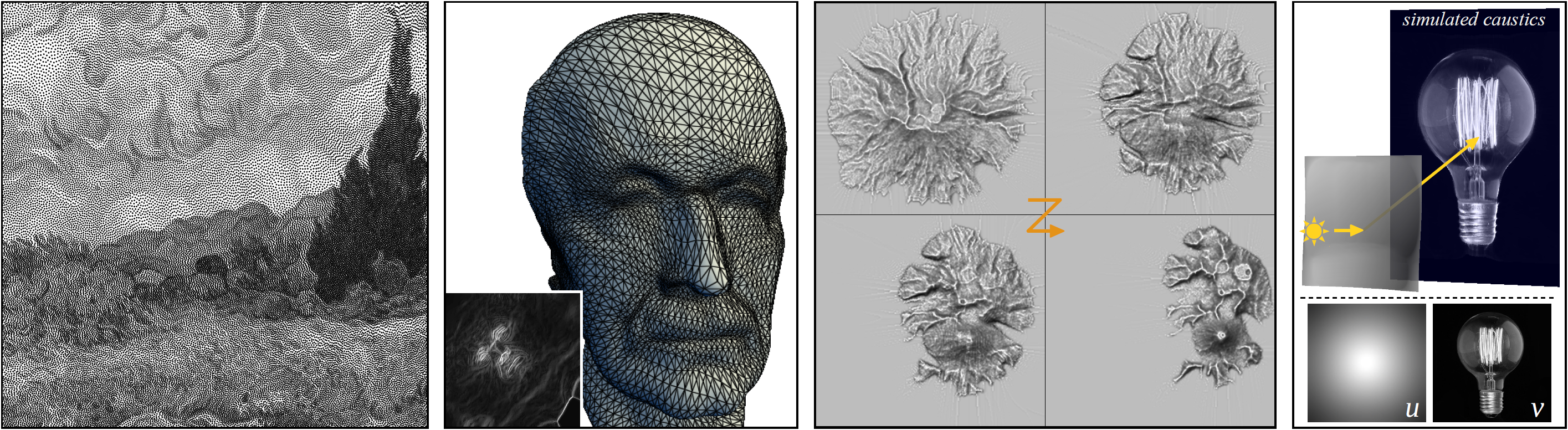
Figure 1. Our fast mass-transport solver enables many applications such as adaptive sampling, surface remeshing, heightfield morphing and caustic design with interactive performance. From left to right: a painting of Van Gogh (A Wheatfield with Cypresses), Max-Planck 3D model courtesy of Max-Planck Institut für Informatik, and volcano heightmaps courtesy of University of Otago.

Abstract

In this paper, we introduce a novel and extremely fast algorithm to compute continuous transport maps between 2D probability densities discretized on uniform grids. The core of our method is a novel iterative solver computing the L2 optimal transport map from a grid to the uniform density in the 2D Euclidean plane. A transport map between arbitrary densities is then recovered through numerical inversion and composition. In this case, the resulting map is only approximately optimal, but it is continuous and density preserving. Our solver is derivative-free, and it converges in a few cheap iterations. We demonstrate interactive performance in various applications such as adaptive sampling, feature sensitive remeshing, and caustic design

Video

Citation


@article{otmap_2018,
  author    = {Nader Georges and Gael Guennebaud},
  title     = {Instant Transport Maps on 2D Grid},
  journal   = {ACM Trans. Graph.},
  year      = {2018},
  volume    = {37},
  number    = {6},
  articleno = {249},
  numpages  = {13},
  doi       = {10.1145/3272127.3275091}
}